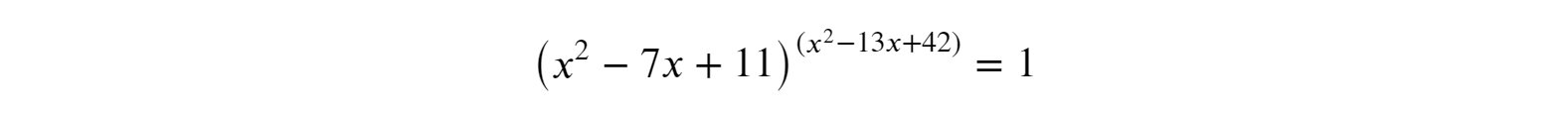In this article, we will discuss about how to solve a polynomial equation. This equation is a quadratic equation raised to the power of another quadratic equation.
A Quadratic Equation Raised to the Power of A Quadratic Equation
Imagine this, there is a quadratic equation raised to the power of another quadratic equation. You might think, what on earth is this? It must be very insane! How can we solve this kind of equation?
Well, believe it or not? The trick is indeed very easy.
Without further ado, here is the equation:
\[\left( x^2 - 7x + 11 \right)^{(x^2 - 13x + 42)} = 1 \label{eq:quad_power_quad}\]The goal is to find the value of $x$ which satisfies the equation above.
Okay, fine. Now, where should I start from?
Case 1: $a^0 = 1$
This is a very fundamental concept in high school maths. It should look familiar: any number, $a$ raised to the power of $0$ equals to $1$. Looking back at our equation, we can quickly recognize that the value on the right hand side is $1$.
Therefore, we make the following substitution with the information provided:
\[\begin{align} a &= x^2 - 7x + 11 \notag \\ 0 &= x^2 - 13x + 42 \label{eq:power0} \end{align}\]And guess what? We can solve $\eqref{eq:power0}$ right away! 😀
Let’s move on…
\[\begin{align} x^2 - 13x + 42 &= 0 \notag \\ (x - 6)(x - 7) &= 0 \notag \\ x &= 6, 7 \end{align}\]Good start! We have earned our credit by obtaining our first two values of $x$.
But, wait! These are only the first two values of $x$. Then, what’s next?
Be patient, let’s keep calm and proceed to the second case! ☕
Case 2: $1^b = 1$
Again, this should be another fundamental concept taught in high school maths class: $1$ raised to the power of any number, $b$ remains as $1$. Similarly, we can make the following substitution with the information provided:
\[\begin{align} 1 &= x^2 - 7x + 11 \label{eq:equal_to_1} \\ b &= x^2 - 13x + 42 \notag \end{align}\]At this point, the next step should look easy.
\[\begin{align} x^2 - 7x + 11 &= 1 \notag \\ x^2 - 7x + 10 &= 0 \notag \\ (x - 2)(x - 5) &= 0 \notag \\ x &= 2, 5 \end{align}\]Voila! We have earned another credit by obtaining another two values of $x$ that satisfies $\eqref{eq:quad_power_quad}$.
To summarize, these are the solutions for now: $x = 2, 5, 6, 7$
You might think…
So far, we already have all possible cases covered, don’t we?
Well, think again. 🙂
There is one more case to consider:
Case 3: $(-1)^{2c} = 1$
This completes the final piece of puzzle to our solution.
The complete solution should be: $x = 2, 3, 4, 5, 6, 7$
Amazing! But, how do we know if we are doing it all correct?
Well, we can always plug in any value from the list back into $\eqref{eq:quad_power_quad}$ to verify our solutions.
Cheerio!
References
- Fast and Easy Maths! “99% fail to answer this question asked in an entrance exam! See if you can!” YouTube, Jul. 20, 2020. [Video file] Available: https://www.youtube.com/watch?v=tY549tYv3yI [Accessed: Jul. 25, 2020].
- T. (https://math.stackexchange.com/users/271938/tusky), “Solution to the equation of a polynomial raised to the power of a polynomial,” Mathematics Stack Exchange. [Online]. Available: https://math.stackexchange.com/q/2943102 [Accessed: Jul. 25, 2020].